Maths Dictionary



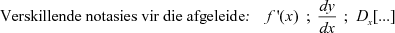
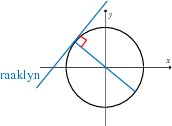
bv. 'n raaklyn aan 'n sirkel is loodreg op 'n radius van daardie sirkel, by die raakpunt
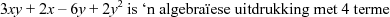
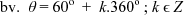


(bv. 'n maksimum van 12 uur is beskikbaar om 'n produk te vervaardig of ten minste 5 eenhede moet per dag verkoop word)
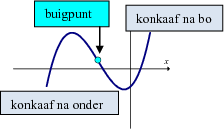
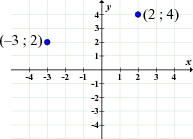
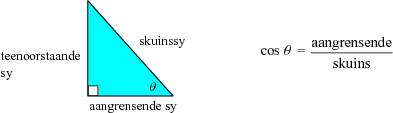
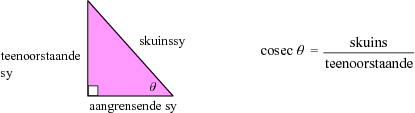
bv. y = x3 + 2x2 - x - 4
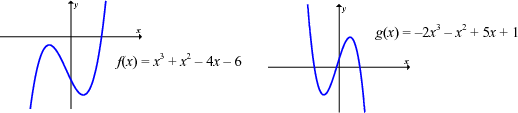
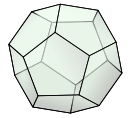
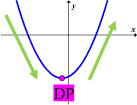
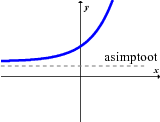
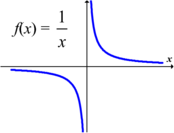
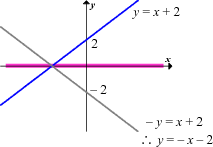
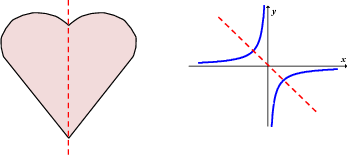
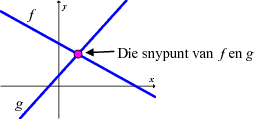
Op die grafiek: As jy 'n vertikale of 'n horisontale lyn oor die grafiek beweeg, dan sal beide die grafiek net een keer sny.
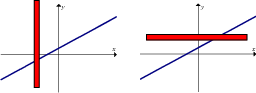
(bv. 12% p.j. jaarliks saamgestel)
bv. om 'n dobbelsteen te rol

Formule: A = P(1 + in)
bv. jy kan nie voorspel watter getal jy gaan kry as jy 'n dobbelsteen rol nie
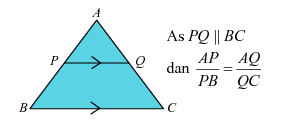

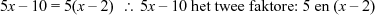
of
As f(b/a) = 0 dan is ax – b 'n faktor van f(x)
bv. x + 4 is 'n faktor van f(x) = x2 - 2x - 8, want f(-4) = (-4)2 - 2(-4) - 8 = 0

bv. 5! = 5 x 4 x 3 x 2 x 1
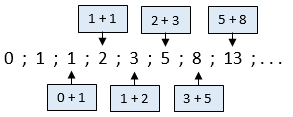
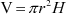

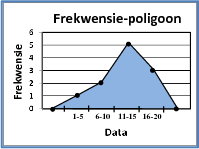
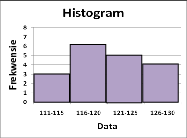
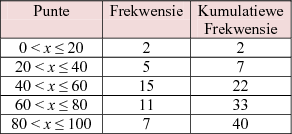
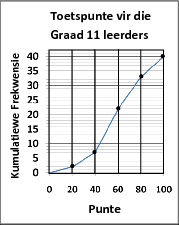
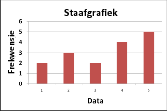
'n Grafiek wat gegroepeerde data vertoon. 'n Frekwensieveelhoek bestaan uit lyne wat die horisontale as met die datapunte met koördinate (klasmiddelpunt ; frekwensie van die klas), verbind.
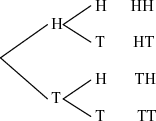
bv. As jy 'n dobbelsteen rol (6 uitkomstes) en 'n muntstuk opskiet (2 uitkomstes), dan is daar altesaam 12 (6 x 2) moontlike uitkomstes.
bv. laat gebeurtenis A 'n ewe getal wees as jy 'n dobbelsteen rol
L.W. Ons sê 1 gebeurtenis en 2 gebeurtenisse of 2 gebeure

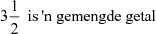
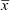

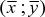



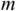
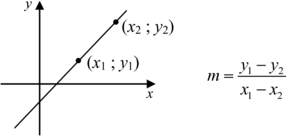


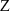
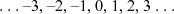
(bv. 1 + 4 = 5 en 9 + 16 = 25 is onvolledige bewyse dat die som van twee volkome vierkante nie 'n volkome vierkant is nie)

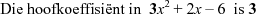


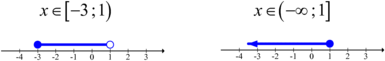

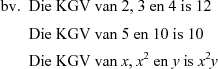
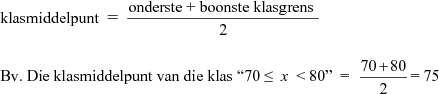
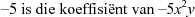

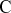
Reël:
P(nie A) = 1 - P(A)
of
As A en B komplementêre gebeurtenisse is, dan P(B) = 1 - P(A) of P(A) = 1 - P(B).

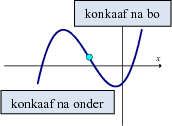
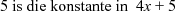
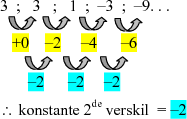
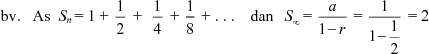


(bv. maksimum wins en minimum koste)

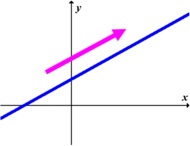
bv. lyn AB:
Sien ook regressielyn.
bv. lynstuk AB:


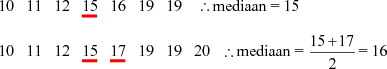
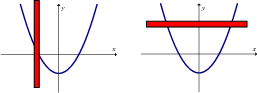
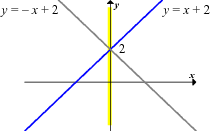
Op 'n grafiek: As jy 'n vertikale lyn oor die grafiek beweeg, sny die lyn die grafiek net een keer, maar as jy 'n horisontale lyn oor die grafiek beweeg, sny die lyn die grafiek meer as een keer.
(bv. 100 ; 50 ; 25 ; 12,5 ; . . .)
(bv. 100 + 50 + 25 + 12,5 + . . .)
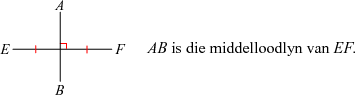
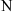
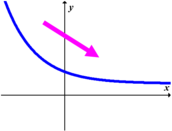
Die regressielyn het 'n negatiewe gradiënt, i.e. die lyn is dalend.

(bv. 12% p.j. maandeliks saamgestel)

bv. om kop te kry as jy 'n muntstuk opgooi en om 6 te kry as jy 'n dobbelsteen rol
Omdat hierdie onafhanklike gebeurtenisse is, kan ons die produkreël gebruik: P(H en 6) = P(H) x P(6)
bv. ewe en onewe getalle is onderlinguitsluitend, want getalle kan nie ewe en onewe op dieselfde tyd wees nie
As A en B onderlinguitsluitend is, dan P(A en B) = 0.
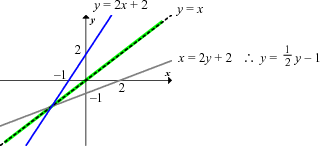
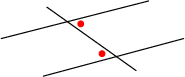
NB: Wanneer 'n ongelykheid opgelos word, verander die rigting van die ongelykheidsteken as ons met 'n negatiewe getal maal of deel.
bv. As gebeurtenis A is om 7 te kry as jy 'n dobbelsteen rol, dan P(A) = 0
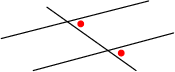
Ons kan die reël vir enige tipe gebeurtenisse gebruik, maar as die gebeurtenisse onderlinguitsluitend is, hoef ons nie die " - P(A en B)" deel by te voeg nie. Dit is omdat P(A en B) = 0 vir onderlinguitsluitende gebeurtenisse.
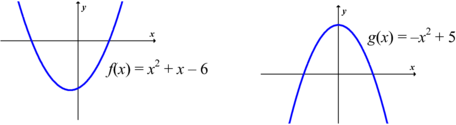

Ook bekend as "die lyn van beste passing".


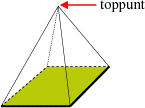
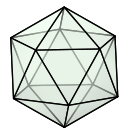
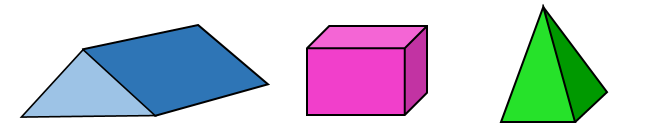
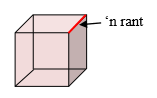
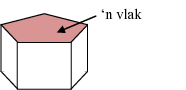
- vlakke wat kongruente reëlmatige veelhoeke is
- kante wat almal dieselfde lengte het
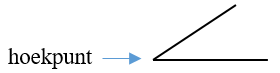
- dieselfde aantal kante wat by elke hoekpunt ontmoet
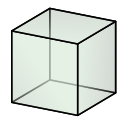
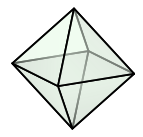
Die Platoniese vorms is die tetraëder, die heksaëder (kubus), die oktaëder, die dodekaëder en die ikosaëder.

NB: Siliders, keëls en sfere is nie poliëders nie.
Die regressielyn het 'n positiewe gradiënt, i.e. die lyn is stygend.

bv. priemfaktore van 24 = 2 x 2 x 2 x 3 = 23.3

Ons gebruik dit met onafhanklike gebeurtenisse.
bv. as jy 'n dobbelsteen 20 keer rol gee dit 20 proewe

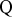
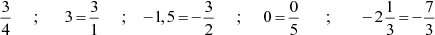
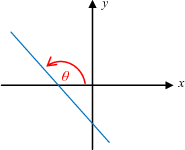
(bv. sin 240o = sin (180o + 60o) = -sin 60o)
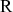
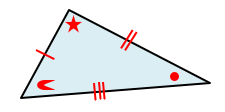
(bv. 'n gelyksydige driehoek het drie gelyke sye en al drie die hoeke is 60o)

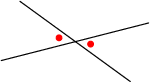
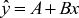
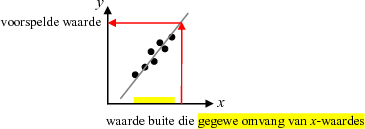
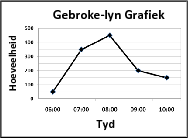
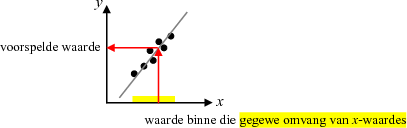
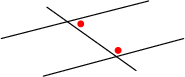
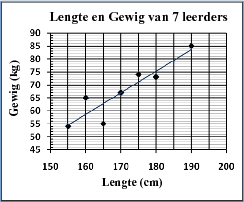
'n Lyn wat deur die punte op 'n spreidingsdiagram getrek word om die verwantskap tussen die twee veranderlikes wat bestudeer word, op te som.
Hierdie lyn kan ook gebruik word om voorspellings en skattings te maak.

(bv. 5 ; 1 ; -3 ; -7 ; . . . )
(bv. 1 + 6 + 11 + 16 + . . .)
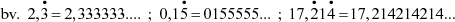

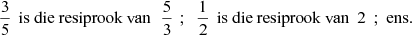
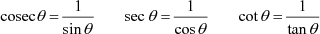
of
As f(x) deur ax- b gedeel word, dan is die res f(b/a)
bv. Die res as f(x) = x2 - 2x - 8 deur x + 1 gedeel word is -5, want f(-1) = (-1)2 - 2(-1) - 8 = -5

(bv. 6 = 1 × 6 en 6 = 2 × 3 . Dit sê vir ons dat 6 'n saamgestelde getal met faktore 1, 2, 3 en 6 is.)
Formule: A = P(1 + i)n
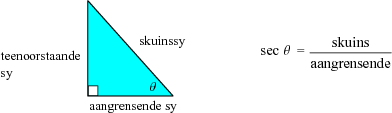
bv. As gebeurtenis A is om 1, 2, 3, 4, 5, of 6 te kry as jy 'n dobbelsteen rol, dan P(A) = 1


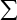

bv. die lengte en gewig van leerders (tweeveranderlike data)

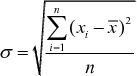
(bv. Translasies, refleksies en rotasies is almal starre transformasies. 'n Vergroting is nie star nie, want die grootte van die voorwerp verander.)
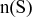
bv. n(S) = 6 as ons 'n dobbelsteen rol, want daar is 6 uitkomstes: 1, 2, 3, 4, 5 of 6


bv. straal AB:
bv. Daar is 3 terme in 2a - 4b + 6 maar daar is net 1 term in 3(x-2) en in (x-1)(x+3)2
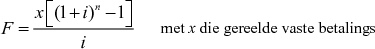

(bv. lengte en gewig van leerders)
bv. om 6 te kry as jy 'n dobbelsteentjie rol
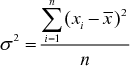

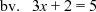

Kyk vir 'n Z of 'n N.


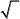
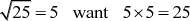

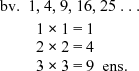
bv. 1 - 3 + 5 - 4 + 9 . . .